Naming Game

The simplest version of the Naming Game is played by a population of N agents trying to bootstrap a common vocabulary for “naming” a certain number of objects in their environment. The objects can be people, things, relations, colors, web sites, pictures, or music files – any kind of entity for which a population aims at developing a naming convention.

Each player is characterized by an inventory of word-object associations he/she knows. All the inventories are initially empty at the first time step (t = 0). At each time step (t = 1, 2, ..) two agents are picked at random; one acts as speaker and the other as hearer. They engage in a naming game interaction according to the following rules:

1. The speaker selects an object or meaning from the current context..The speaker retrieves a word from its inventory associated with the chosen object. If the speakers’ inventory is empty, they invent a new word.
2. The speaker transmits the selected word to the hearer.
3. If the hearer has the word in its inventory for the relevant object or meaning, the interaction is a success and both players maintain only the winning word in their inventories, discarding all other names for that object or meaning.
4. If the hearer does not have the word named by the speaker in its inventory, or the word is associated to a different object, the interaction is a failure and the hearer updates its inventory by adding an association between the new word and the object.

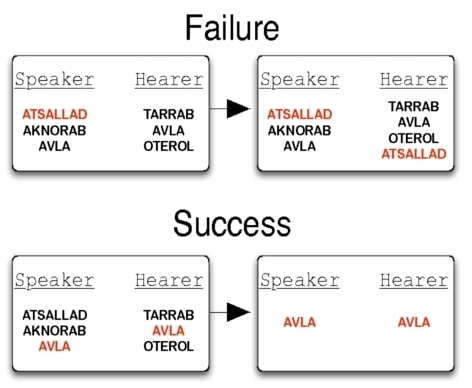
Figure 1. Examples of the dynamics of the inventories in a failed (top) and a successful (bottom) game. The speaker selects the word highlighted. If the hearer does not possess that word he adds it to his inventory (top). Otherwise both agents erase their inventories only keeping the winning word (bottom).

Example: Naming Colors

The small demonstration below illustrates the game with a group of agents interacting to evolve names for a set of color meanings according to the rules described above. The graph on the bottom shows success over time for each color; success is at first low for all colors, but increases over time, indicating that a shared name for the color is emerging.

Figure 2.  Speed up time by changing the Interaction Rate, or change the number of agents or colors to see how this changes the rate at which consensus is reached among the agents. The large bar on the right indicates average success over the population for a sliding window of 100 interactions. The “eyes” of the agents indicate their individual success over the same window. When the population has reached consensus on a name for a color, it brightens.

The Main Results

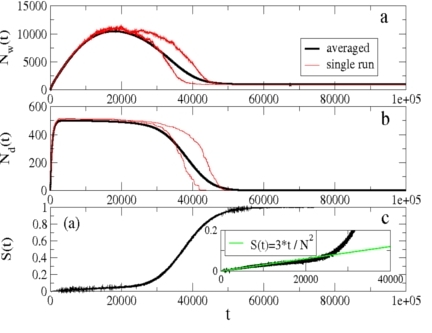
The main results of the Naming Game dynamics for a single meaning or object are summarized in Figure 3. The most interesting properties of these dynamics are the evolution over time of the total number of words in inventories across the population, N_w(t), the number of different words N_d(t), and the communicative success rate S(t). Although in these simulations only two agents interact at each time step, the model also extends to cases where any number of agents interact simultaneously.

Figure 3. Total number of words present in the system, N(t); b) Number of different words, N_d(t) c) Success rate S(t), i.e., probability of observing a successful interaction at time t. The inset shows the linear behavior of S(t) on a shorter timescale. The system reaches the final absorbing state, described by N_w(t) = N, N_d(t) = 1 and S(t) = 1, in which a global agreement has been reached.